A typical Reusable Launch Vehicle (RLV) flies through continuum flow regions at low altitude, fully rarefied flows at high altitude, and mixed continuum-rarefied flows in transition. In particular, hypersonic reentry vehicles at high altitude show tremendous increases in density close to the body (Figure 1) while the free stream is still rarefied. This phenomenon results in a Knudsen number close to the body, which is several orders of magnitude smaller than the free stream Knudsen number. For these high speed and high enthalpy flows, experimental data are nearly impossible to obtain, so accurate computational methods to predict both aero and thermal loading are invaluable.

Figure 1.- Kistler RLV Density Contour Plot
There are two CFD methods (Figure 2) that are used to model fluid flows: the continuum method such as the Navier-Stokes equations, which treats the fluid as a continuous substance at the macroscopic level, and the particle method such as the Boltzmann equation, which retains the physical idea that the fluid is composed of a collection of discrete molecules at the microscopic level. However, these two methods have some key differences long recognized in the continuum and particle methodologies.
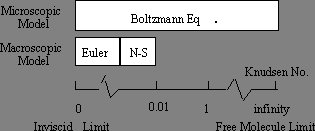
Figure 2.- Mathematical Models of Fluid Motion
The Direct Simulation Monte Carlo (DSMC) method is one of the particle methods that is efficient enough to handle large-scale flow simulations. It has evolved over a period of 35 years and become a useful tool in the field of rarefied gas dynamics. Theoretically, the DSMC method is able to provide flow solutions in both rarefied and continuum fluid media. However, because a particle method uses huge numbers of computational molecules to represent the gas being modeled, it requires large amounts of computer memory and CPU time. It becomes inefficient to model the flow in high-density regions close to the body even with the fastest supercomputer today. On the other hand, the continuum Navier-Stokes method provides an efficient method for flows in the continuum regimes. In general, the DSMC particle method is used to simulate highly rarefied flows, where continuum methods such as the Navier-Stokes equations become invalid. Therefore, a combination of the particle method and the continuum method is a natural path to provide a computationally efficient method for designing RLVs in all flow regimes.
In kinetic theory, moments of the Boltzmann equation connect the Boltzmann equation to the Euler/Navier-Stokes equations. Taking both the collision invariant and the Maxwellian velocity distribution function into the moment equations leads to the Euler equations. Similarly, inserting the Chapman-Enskog velocity distribution function into the moment equations leads to the Navier-Stokes equations (Figure 3). An important result of the Boltzmann equation is that molecular collisions drive the velocity distribution along in an irreversible path. This results from the phenomena of molecular chaos. Important properties projected from the Boltzmann equation level onto the Navier-Stokes equations level are the upwind and entropy conditions. The H-theorem in kinetic theory is the equivalent of the entropy condition of continuum thermodynamics.
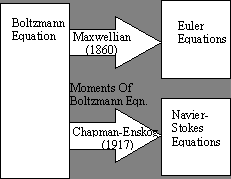
Figure 3.- Relationships of CFD Governing Equations
There are two strategies for approaching the Boltzmann equation: the case of particle algorithms or moment algorithms. The particle algorithms compute the particle velocity in the flow field directly, and this information is used to compute the moments of particle velocity (such as density, temperature, pressure, etc.) as needed in the flow field. Bird’s DSMC and Prendergast’s kinetic methods are examples of such kinetic-based particle algorithms. However, computational efficiency of the particle algorithms is low compared to the moment algorithms. In addition, collision terms and boundary conditions for nonequilibrium flows are difficult to implement in particle methods. It often is necessary to assume a less accurate local Maxwellian velocity distribution for the boundaries. On the other hand, the moment algorithms take moments of the Boltzmann equation to produce the moment equations analytically, while the macroscopic properties are obtained by solving the moment equations such as Euler or Navier-Stokes equations. Deshpande’s and Chou-Baganoffs' kinetic-based methods belong to this approach (Figure 4).

Figure 4.- Connections of Kinetic-based CFD Algorithms
Unlike continuum upwind schemes, which are based on the eigenvalues of the total flux Jacobian in characteristic wave theory, a kinetic-based scheme relies on the signal propagation associated with the (microscopic) particle velocity. If the eigen-based algorithms are considered as analog technology (wave theory) in CFD, then the kinetic-based CFD algorithms will be the digital technology (particles-collision kinetic theory) for the future.
Commercial Applications: A long-range goal at NEAR is to develop an effective kinetic-based CFD algorithm with multiblock capabilities for viscous flows with proper finite-rate chemistry models. This research will not only provide the building blocks for such a capability, but will also provide new technologies to expand the range of CFD applications to mixed continuum-rarefied hybrid flow regimes.
References:
1. Chou, S. Y., "Kinetic Flux Vector Splitting for the Navier-Stokes Equations," Ph.D. Thesis, Stanford University, Jun. 1995.
2. Chou, S. Y. and Baganoff, D., "Kinetic Flux Vector Splitting for the Navier-Stokes Equations," Journal of Computational Physics, Vol. 130, Jan. 1997, pp. 217-230.
3. Chou, S. Y., "On the Mathematical Properties of Kinetic Split Fluxes," AIAA 2000-0921, Jan. 2000.
4. Chou, S. Y., "Applications of Kinetic Fluxes to Hybrid Continuum-Rarefied Methods," Panel on Continuum and Rarefied Flight Regimes (Invited), AIAA 37th Thermophysics Conference, Jun. 2004. Click to Download Presentation, 15MB





